Applications of Conformal Geometric Algebra in Character Animation
Geometric Algebra (GA) provides a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. The Conformal model of GA gives the ability to describe algorithms in a geometrically intuitive and compact manner since basic entities, such as spheres, lines, planes and circles, are simply represented by algebraic objects. GA is also more numerically stable and more efficient than rotation matrices making it popular for applications in computer graphics, character animation, and robotics. Rotors are simpler to manipulate than Euler angles and avoid the problem of gimbal lock (Gimbal lock is a common problem associated with Euler angles and occurs because two axes become aligned during rotational operations, producing unexpected behavior since one degree of freedom is lost).
For a detailed introduction to Geometric Algebra, a brief outline of the Conformal model of Geometric Algebra (CGA), and ways to examine how the Conformal model can represent geometric primitives such as points, lines, circles, planes and spheres, please refer to the second chapter of my PhD thesis Tracking and Modelling Motion for Biomechanical Analysis. In the Appendix, we also present some trigonometric solutions using Conformal Geometric Algebra, such as how to find the Nearest Point on a Circle from a Point in Space, the Nearest Point on a Line from a Circle, the Nearest Point on a Line from a Sphere, and the Nearest Point on a Sphere from a Point in Space.
Dual Quaternions is also part of the Conformal Geometric Algebra (CGA). To understand the relationship between dual quaternions and CGA, it is helpful to break down the concepts:
Quaternions: These are extensions of complex numbers used to represent rotations in three-dimensional space. Quaternions are expressed in the form q = w + xi + yj + zk, where w, x, y, and z are real numbers, and
i, j, and k are imaginary units.
Dual Numbers: These extend real numbers with an additional element 𝜖 where 𝜖^2 = 0 (but 𝜖 ≠ 0). A dual number is of the form a + bϵ, where a and b are real numbers.
Dual Quaternions: These combine the concepts of quaternions and dual numbers. A dual quaternion is of the form q_d = q_1 + ϵq_2, where q_1 and q_2 are quaternions. Dual quaternions are useful in representing rigid body transformations (rotations and translations)
in three-dimensional space.
Geometric Algebra (GA): This is a mathematical framework that generalizes complex numbers, quaternions, and several other algebraic systems. GA is used for computations involving geometry, such as rotations and reflections.
Conformal Geometric Algebra (CGA): This is an extension of geometric algebra that is particularly well-suited for describing transformations in Euclidean space, including translations, rotations, dilations,
and inversions. CGA operates in a higher-dimensional space, allowing for a unified representation of various transformations.
In CGA, points, lines, planes, and spheres are represented in a way that allows for seamless application of geometric transformations. Dual quaternions can be embedded within this framework because they can represent rigid body motions, which are a subset of the transformations that CGA can handle.

Pose Representations for Deep Skeletal Animation
Nefeli Andreou, Andreas Aristidou, Yiorgos Chrysanthou
Computer Graphics Forum, Volume 41, Issue 8, December 2022.
Presented at ACM SIGGRAPH/ Eurographics Symposium on Computer Animation, SCA'22, September, 2022.
In this work we present an efficient method for training neural networks, specifically designed for character animation. We use dual quaternions as the mathematical framework, and we take advantage of the skeletal hierarchy, to avoid rotation discontinuities, a common problem when using Euler angle or exponential map parameterizations, or motion ambiguities, a common problem when using positional data. Our method does not requires re-projection onto skeleton constraints to avoid bone stretching violation and invalid configurations, while the network is propagated learning using both rotational and positional information.
CGA, a mathematical framework for motion continuity in deep neural networks
Andreas Aristidou
In Proceedings of the International Conference on Empowering Novel Geometric Algebra for Graphics & Engineering (ENGAGE'20), Geneva, Switzerland, September 2020.
Generating human motion in computational modeling is challenging due to its continuous, high-dimensional, and expressive nature. Traditionally, articulated motion is managed by rigging skeleton bones and modifying joint angles over time. Recent advances in deep learning have shown promise in controlling such characters using various neural network architectures. However, representing 3D rotations in low-dimensional Euclidean spaces is discontinuous, leading to erroneous motions in neural network outputs. Researchers often use positional data to mitigate this, but it has ambiguity issues and requires additional layers for accuracy. This work explores using conformal geometric algebra (CGA) to ensure continuity in motion representation for deep neural networks. It compares CGA with other frameworks like Euler angles and quaternions in terms of motion smoothness and presents a method for converting motion files to and from CGA for easier neural network integration.
A Conformal Geometric Algebra framework for Mixed Reality and mobile display
Margarita Papaefthimiou, George Papagiannakis, Andreas Aristidou, Marinos Ioannides
In Proceedings of the 6th Conference on Applied Geometric Algebra in Computer Science and Engineering (AGACSE'15), Barcelona, Spain, July 2015.
Recent advances in user interface and mobile computing have enhanced our ability to interact with information through virtual characters, using technologies like Virtual Reality (VR) and Augmented Reality (AR). VR immerses users in 3D computer-simulated environments, while AR overlays computer-generated sensory inputs onto the physical world. Both rely on interactive devices, computer vision, and mobile displays to create an immersive experience. However, they face challenges with interpolation errors in tracking user movements, gesture inputs, and animation blending of virtual characters.
This talk proposes enhancing the conformal model of Geometric Algebra (CGA) for better control in immersive and virtual technologies like head-mounted displays and smartphones. CGA offers a robust mathematical framework for representing and computing object orientations, rotations, and translations, surpassing traditional linear and quaternion methods. By using CGA, we can unify and improve camera transformations, replace quaternions with more efficient CGA rotors, and seamlessly blend animations, resulting in a more stable and realistic real-time mobile mixed reality experience.
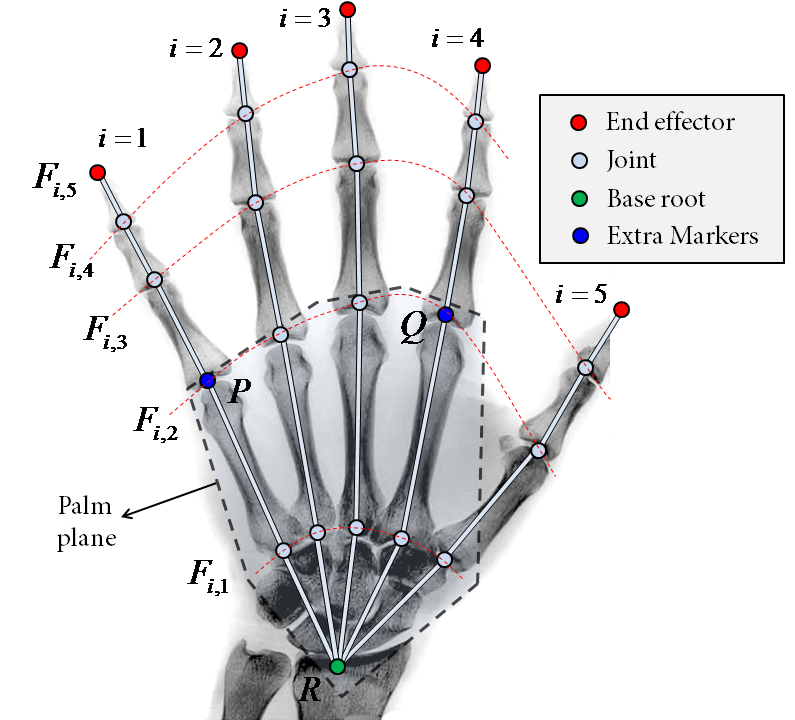
Inverse Kinematics solutions using Conformal Geometric Algebra
Andreas Aristidou, Joan Lasenby
Guide to Geometric Algebra in Practice, L. Dorst and J. Lasenby (Eds), pages 47-62, Springer Verlag, 2011.
An iterative Inverse Kinematics solver is implemented using Conformal Geometric Algebra. We use a human hand as an example of implementation where a constrained version of the IK solver is employed for pose tracking. The hand is modelled using CGA, taking advantage of CGA's compact and geometrically intuitive framework, that basic entities in CGA, such as spheres, lines, planes and circles, are simply represented by algebraic objects.
Project Description
In this paper, CGA was chosen to describe a fast iterative Inverse Kinematics solver (FABRIK) since it simpifies the mathematical model (basic entities, such as spheres, lines, planes and circles, are simply represented by algebraic objects). A simple and efficient methodology for tracking and reconstructing 3d hand poses using a markered optical motion capture system is also presented. It is assumed that the hand geometry, meaning the initial joint configuration of the hand, is known. Also, it is assumed that the hand palm is flat and that the orientation of the hand is given by the hand palm. The model is highly constrained with rotational and orientational constraints implemented using CGA. FABRIK was then applied to fit the rest of the joints; the end effector positions are markers which are attached at the end of each finger and they are captured using an optical motion capture system (Phasespace). The proposed IK solver and hand model are real-time implementable and the resulting motion is smooth and natural.
© 2025 Andreas Aristidou